다익스트라 알고리즘(베이직 버전) - 핵심코드
- 알고리즘/코테 알고리즘 정리 노트
- 2020. 9. 23. 10:55
static void dijkstra(int start) {
d[start] = 0;
visited[start] = true;
for(int j = 0; j < graph.get(start).size();j++) {
d[graph.get(start).get(j).index] = graph.get(start).get(j).distance;
}
for(int i = 0; i<n-1;i++) {
int now = get_smallest_node();
visited[now] = true;
for(int j = 0; j < graph.get(now).size();j++) {
int cost = d[now] + graph.get(now).get(j).distance;
if (cost < d[graph.get(now).get(j).index]) {
d[graph.get(now).get(j).index] = cost;
}
}
}
}자바로 구현된 이 코드는 다익스트라 알고리즘의 핵심 코드다.
시작은 0으로 초기화 시켜주고
방문했다는 표시를 해줍니다.
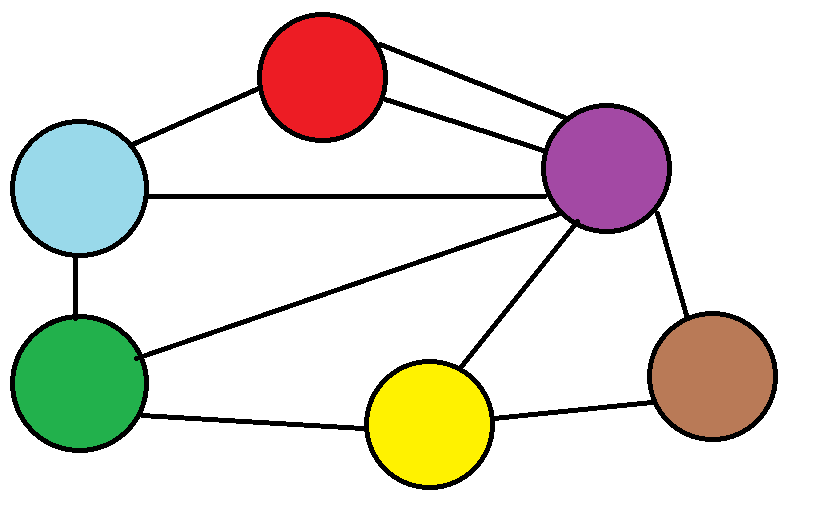
이러한 그래프가 있다고 가정해봅시다. 현재는 값은 일부러 생략했지만...
아무튼... 파란색공부터 시작한다고 가정합시다.
그러면 파란공은 자기자신으로 가는 거리까지 걸리는 간선의 길이는 0입니다.
왜냐하면 이동할 필요가 없기 때문이죠.
이동을 하지 않았다고는 하지만, 방문은 한 샘이니... 방문했다고 표시합니다.
첫 번째 반복문은 첫번째 노드(파란 공) 에서 갈 수 있는 노드의 갯수입니다.
그림을 보면 빨간색, 초록색, 보라색쪽으로 갈 수 있다는 사실을 알 수 있습니다.
이 부분이 햇갈릴 수 있어서 가지고 왔습니다.
d[graph.get(start).get(j).index] = graph.get(start).get(j).distance;
간단히 코드를 바꿔보면
Node next = graph.get(start).get(j);
d[next.index] = next.distance;이런식으로 중복을 제거할 수 있었습니다.
아무튼 제가 말하고 싶은건 next.index가 빨간색, 보라색, 초록색의 값을 뜻합니다.
그리고 d는 최소 거리라 생각해도 될 것 같습니다.
즉, 다음 노드의 인덱스 위치에 그 노드의 거리를 삽입하는 것으로 해석할 수 있습니다.
자 이제 이런식으로 다음 노드도 진행해 봅시다.
for(int i = 0; i<n-1;i++) {
int now = get_smallest_node();
visited[now] = true;
for(int j = 0; j < graph.get(now).size();j++) {
int cost = d[now] + graph.get(now).get(j).distance;
if (cost < d[graph.get(now).get(j).index]) {
d[graph.get(now).get(j).index] = cost;
}
}
}어차피 첫번째 노드는 사용하였기 때문에 n-1로 해둡니다. i를 1로 하구 n까지해도 무방할 것 같습니다. 왜냐하면 i를 사용하는 곳이 없기 때문이죠.
어느 노드에서 최소 거리를 가지는지 구하는 메소드를 구현합니다.
지금까지 이동한곳은 총 3군데, 빨강, 보라, 초록입니다. 그리고 이 값들은 d(최소 거리)배열에 저장이 되있죠.
따라서 지금 상태로는 이들은 각각의 최소거리라고 할 수 있습니다.
static int get_smallest_node() {
int min_value = INF;
int index = 0;
for (int i = 1; i < n + 1; i++) {
if (d[i] < min_value && !visited[i]) {
min_value = d[i];
index = i;
}
}
return index;
}
kㅃ코드는 다음과 같습니다.
근데 어떤 노드가 최소거리인지 구하는 함수를 봅시다. i값이 계속 증가하는 형태를 보이는 것으로 봐서 최소거리의 노드는 3개가 아니라 1개만 등장하는 듯합니다.
예륻 들어 초록색이라고 해봅시다.
그러면 초록색은 파란색에서의 최소 거리를 가지는 노드라고 해도 될 것 같습니다.
이제 현재 값에서 다음 노드로 갈 거리를 더해줍니다. 그러면 값이 증가가 됩니다.
이제 이렇게 하고 종료일까요?
아닙니다.
만약, 파란 노드에서 보라색 노드를 간다고 생각해봅시다. 그런데 파란 노드에서 보라색 노드로 가는 길이가 더 짧다면
굳이 갱신할 필요는 없어집니다. 반대라면 당연히 갱신 시켜줘야합니다.
여기서 의문인점은 빨강과 보라는 이대로 삭제가 되는지 오해할 수 있다고 생각합니다.
왜냐하면 파란 노드에서 초록색 노드만 사용했기 때문이죠. 하지만 이들은 이미 d배열에 저장이 되어있습니다. 따라서
다른 배열의 위치의 값이 다른 노드로 값이 커지고, 최솟값을 찾는다면 당연히, 빨강 노드 또는 보라색 노드을 찾게 될겁니다. 물론, 초록 노드가 이동했기 때문에 후보군이 늘어난 것은 사실이긴 합니다.하지만... 가장 짧은 노드이 길이만 구하면 되기 때문에 이것은 그렇게 큰 문제가 되지 않습니다.
정리하자면
초기 -> 검색 -> 최소 -> 검색 -> 최소 -> 검색...
이런식으로 동작되는 것 같습니다. 뭐 이건 이해가 되지 않아도 상관없습니다.
마지막으로 방문은 그 노드에 방문해서 생기는 것이 아니라 그 노드에서 시작할때 발생하는 겁니다.
다익스트라 알고리즘은 최단거리를 구하는 알고리즘으로 잘 알려져 있지만,
간선(노드와 노드 사이)의 길이가 음수라면 불가는하다고 합니다.
참고로 노드의 갯수가 10000개를 넘어가면 이 코드로 해결하기 어렵다고 합니다. 이 코드의 시간 복잡도는 O(V^2)입니다.
'알고리즘 > 코테 알고리즘 정리 노트' 카테고리의 다른 글
| 개선된 다익스트라 알고리즘 (0) | 2020.09.23 |
|---|---|
| 어딘가 잘못된 힙...(진짜 잘못됨) (0) | 2020.09.23 |
| 가장 긴 증가 하는 부분 수열 (0) | 2020.09.21 |
| 다이나믹 프로그래밍 (1) (0) | 2020.09.20 |
| 자바 조합(combination) 정리 (0) | 2020.09.17 |