서로소 집합 알고리즘
- 알고리즘/코테 알고리즘 정리 노트
- 2020. 10. 1. 10:50
솔직히 아직 이것을 왜 사용해야하는지 잘 모르겠다.
일단 설명을 해보자.
서로소는 서로 나누었을 때 1이 나오는 값을 뜻한다.
예를들어 5와 8이라는 숫자를 봤을 때 이들은 서로소이다.
즉, 최대 공약수가 1인 경우가 서로소 라는 뜻이 된다.
만약에, 3이랑 27 같은 경우
최대 공약수가 3이기 때문에 서로소 가 아니다.
서로소 집합을 구하려면
2가지 방법이 필요 하다고 한다.
1. 합집합 연산을 확인라여, 서로 연결된 두 노드를 확인한다.
2. 모든 합 집합 연산을 처리 할 때까지 1번 과정을 반복한다.

현재 전체는 위와 같다.
그리고 현재 합집합은 다음과 같이 나와 있다.
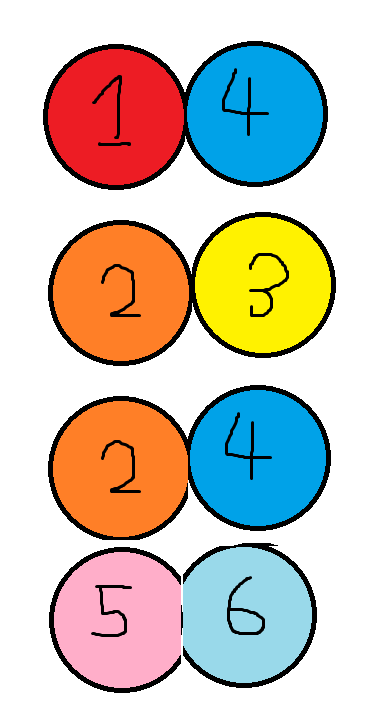
이제 1과 4, 2와 3등은 하나의 집합이 된다.
여기서 중요한 점은 숫자가 낮은 숫자가 부모 노드라고 한다.
초기 부모 노드의 값은 자기 자신이다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 |
위 그림을 보면 3과4의 부모 노드 값이 수정이 필요하다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 2 | 1 // 2 ???? | 5 | 5 |
이런식으로 나오는데... 4를 주목해보면 1과 2둘다 부모 노드를 가질 수 있다.
어떻게 수정하면, 될까?
여기서 더 작은 값은 1이 된다. 그렇기 때문에 이렇게 해도 될까?
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 2 | 1 | 5 | 5 |
근데 문제는 2도 만족을 시켜야 한다. 위 표로는 그것을 증명하기가 어렵다. 왜냐하면
1은 2보다 크기가 큰 수 이기 때문에 2는 1의 부모 노드가 될 수 없다.
결국,

이렇게 부분집합을 구할 수 있다.
따라서 최종 값은
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 2 | 5 | 5 |
즉 이것을 해석 해보면,
4는 2를 부모로 여기지만 2는 1을 부모로 여긴다.
결국 4도 1을 부모로 여긴다는 논리를 알 수 있다.
그러면 이것을 어떻게 코드로 만들까?
static public int findParent(int[] parent, int x) {
if (parent[x] != x) {
parent[x] = findParent(parent, parent[x]);
}
return parent[x];
}
static void unionParent(int[] parent, int a, int b) {
a = findParent(parent, a);
b = findParent(parent, b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}이렇게 2코드가 핵심이다. 나머지는 입력값과 초기화이기 때문에 생략했다.
지금 첫 번째 메소드에서 부모를 찾고 있다. 이는 union연산을 하게 된다.
왜냐하면 부모 값을 찾다보면 자기 자신과 부모 값이 남게 되는데 이들을 구하기 때문이다.
그런데 왜 return이 int나면... 현재 노드 번호는 배열의 인덱스로 대체하고 있다.
따라서 1번 노드의 부모가 2번 노드다 라면 parent[1] = 2가 된다.(이렇게 될일은 없지만..ㅎㅎ)
이렇게 합집합을 구하면 되는데 문제는...
값이 다른 경우가 발생이 된다.
이는 두 번째 메소드로 이를 해결한다.
a값의 부모 노드를 찾고
b값도 부모 노드를 찾는다.
근데 만약에 b값이 더 크 다면 parent[b] = a에 넣어 주면 된다.
서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다는 특징이 있다고 한다.
하지만 어떤 문제에 써야 하는지 잘 모르겠다.
서로소도 알겠구, 서로소 집합도 알겠는데...
문제가 안 그려진다. ㅜㅜ;; 더 공부하다보면 언젠가 보일꺼라 생각하고 여기서 !
'알고리즘 > 코테 알고리즘 정리 노트' 카테고리의 다른 글
| 위상 정렬 (0) | 2020.10.01 |
|---|---|
| 크루스칼 알고리즘 (0) | 2020.10.01 |
| 다이나믹 프로그래밍 (2) (0) | 2020.09.28 |
| 플로이드 워셜 알고리즘 정리 (0) | 2020.09.24 |
| 개선된 다익스트라 알고리즘 (0) | 2020.09.23 |