위상 정렬
- 알고리즘/코테 알고리즘 정리 노트
- 2020. 10. 1. 14:39
위상 정렬은 정렬 알고리즘의 일종이라고 한다.
위상 정렬은 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용되는 알고리즘이라고 한다.
예를 들어,
커리큘럼이 다음과 같이 존재한다고 가정하자.
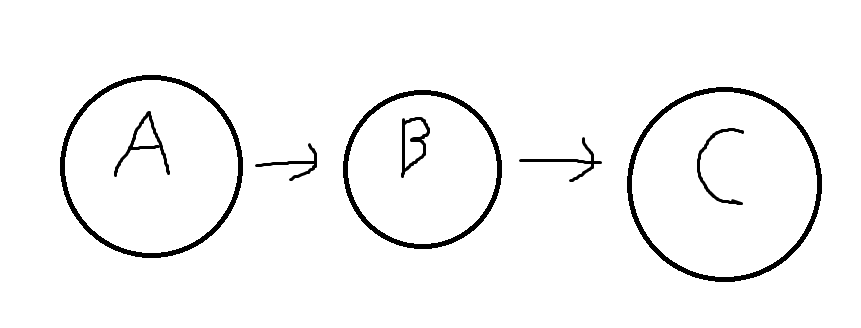
위 그림을 보면 B를 배우기 위해서는 A가 반드시 필요하는 것을 알 수 있다.
위상 정렬을 알기 전에 진입차수라는 것을 알 필요성이 있다.
진입 차수란 특정한 노드로 '들어오는' 간선의 갯수를 의미한다.
따라서 위상 정렬은 다음처럼 동작한다.
1. 진입 차수가 0인 노드가 큐에 넣는다.
2. 큐가 빌때 까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드을 큐에 넣는다.
이것을 코드로 표현해보자.
void topologySort() {
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int now = q.poll();
for (int i : graph.get(now)) {
indegree[i] -= 1;
if (indegree[i] == 0) {
q.offer(i);
}
}
}
}
위 그림을 보면 A과목을 배우기 위해서는 아무것도 학습할 필요가 없다.
아무것도 학습할 수 없다는 것을 0이라고 표현한다.
그런다음 큐에 넣는다.
큐가 빌때 까지 무한 반복한다.
그러면 그래프에 저장된 값들을 찾을 수 있다.
만약, A -> B , A->C라면 B와 C가 나온다.
근데 왜 -1일 할까? 그것은 이제 이것을 배운다는 의미로 해석할 수 있다.
A과목은 배웠기 때문에 B,C를 배울 차례가 되었다.
그래서 1을 빼는거다. 만약, 1을 빼지 않는다면
D도 똑같이 선행 과정이 없다고 하자 또, D -> E가 성립한다면
E과목의 진입 차수 값은 1이 된다. 근데 모든 1을 빼지 않는다면 여기서 애매해진다.
그래서 이 과목을 들었어요 라는 뜻으로 1을 빼는 것이다.
빼고나면 0이기 때문에 그 값을 큐어 넣는것으로 종료한다.
'알고리즘 > 코테 알고리즘 정리 노트' 카테고리의 다른 글
| 배열 90도 회전 (코드만 존재 설명 X) (0) | 2020.10.29 |
|---|---|
| 숫자 회전 (4자리 한정) (0) | 2020.10.20 |
| 크루스칼 알고리즘 (0) | 2020.10.01 |
| 서로소 집합 알고리즘 (0) | 2020.10.01 |
| 다이나믹 프로그래밍 (2) (0) | 2020.09.28 |